Engineering Physics
Lab Report #5
Newton II - Atwood's Machine
Andy Buettner
Mr. Huttlin
![]() Objective
Objective
The Objective of this lab is to study the validity of Newton's third law, Force = Mass * Acceleration, by studying Atwood's Machine.
![]() Materials
Materials
Timer
Atwood's Machine
Complete set of masses
Measuring device
![]() Procedure
Procedure
I) Part 1:
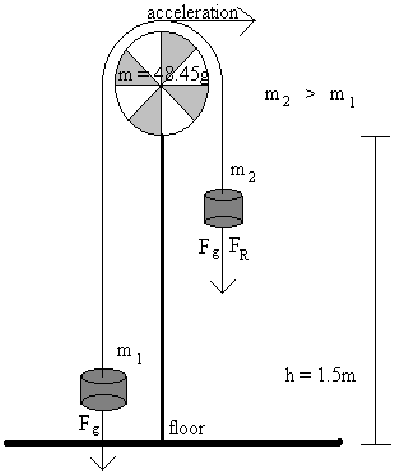
Measure the height, of the system, the mass of each weight tray, and the mass of the pulley system.
Place 1040g of mass on each side.
Remove 10g of mass from one side and place it on the other.
Move the more massive end to the top of the machine.
Time the time it takes for the more massive end to fall to the ground.
Repeat step 5 four additional times and record the results.
Repeat steps 4 through 6 three additional times.
II) Part 2:
Remove all masses from the system.
Place 30g of mass on one side but not the other.
Place 400g of mass on each side of the system
Move the more massive end to the top.
Allow the more massive end to fall and record the time it takes.
Repeat step 5 four additional times.
Repeat steps 4 through 6 three additional times adding an additional 200g of mass to each side.
![]() Data
Data
|
Trial #: |
1 |
2 |
3 |
4 |
Average |
|
Time: |
6.02s |
5.73s |
5.82s |
6.06s |
5.91s |
II) Table 2: Results for 1060g / 1020g mass combination.
|
Trial # |
1 |
2 |
3 |
4 |
5 |
Average |
|
Time: |
4.19s |
4.13s |
4.18s |
4.20s |
4.14s |
4.17s |
III) Table 3: Results for 1070g / 1010g mass combination.
|
Trial #: |
1 |
2 |
3 |
4 |
5 |
Average |
|
Time: |
3.40s |
3.55s |
3.65s |
3.40s |
3.39s |
3.48s |
IV) Table 4: Results for 1080g / 1000g mass combination.
|
Trial #: |
1 |
2 |
3 |
4 |
5 |
Average |
|
Time: |
2.89s |
2.89s |
2.95s |
3.03s |
3.07s |
2.96s |
V) Table 5: Average Results for part 1.
Mass of Left: |
1050g |
1060g |
1070g |
1080g |
Mass of Right: |
1030g |
1020g |
1010g |
1000g |
|
Average Time: |
5.19s |
4.17s |
3.48s |
2.96s |
VI) Diagram 1: Illustration of Atwood's Machine.
VII) Table 6: Results for 400g / 430g mass combination.
|
Trial #: |
1 |
2 |
3 |
4 |
5 |
Average |
|
Time: |
3.03s |
2.93s |
3.36s |
3.43s |
3.08s |
3.17s |
VIII) Table 7: Results for 600g / 630g mass combination.
|
Trial #: |
1 |
2 |
3 |
4 |
5 |
Average |
|
Time: |
3.77s |
3.83s |
3.75s |
3.70s |
3.75s |
3.76s |
IX) Table 8: Results for 800g / 830g mass combination.
|
Trial #: |
1 |
2 |
3 |
4 |
5 |
Average |
|
Time: |
4.21s |
4.37s |
4.30s |
4.34s |
4.21s |
4.29s |
X) Table 9: Results for 1000g / 1030g mass combination.
|
Trial #: |
1 |
2 |
3 |
4 |
5 |
Average |
|
Time: |
4.84s |
4.90s |
4.87s |
4.81s |
4.77s |
4.84s |
XI) Table 10: Average Results for part 2.
Mass of Left: |
430g |
630g |
830g |
1030g |
Mass of Right: |
400g |
600g |
800g |
1000g |
|
Average Time: |
3.17s |
3.76 |
4.29 |
4.84 |
![]() Analysis
Analysis
![]() %
Deviation for part 1:
%
Deviation for part 1:
Trial # |
1050g |
1060g |
1070g |
1080g |
|
1 |
1.86% |
.96% |
2.30% |
2.36% |
|
2 |
3.05% |
.96% |
2.01% |
2.36% |
|
3 |
1.52% |
.24% |
4.89% |
.34% |
|
4 |
2.54% |
.72% |
2.30% |
2.36% |
|
5 |
|
.72% |
2.59% |
3.72% |
![]() %
Deviation for Part 2:
%
Deviation for Part 2:
Trial # |
430g |
630g |
830g |
1030g |
|
1 |
4.42% |
.27% |
1.86% |
0% |
|
2 |
7.57% |
1.86% |
1.86% |
1.24% |
|
3 |
5.99% |
.27% |
.23% |
.62% |
|
4 |
8.20% |
1.60% |
1.17% |
.62% |
|
5 |
2.84% |
.27% |
1.86% |
1.45% |
![]() Graph
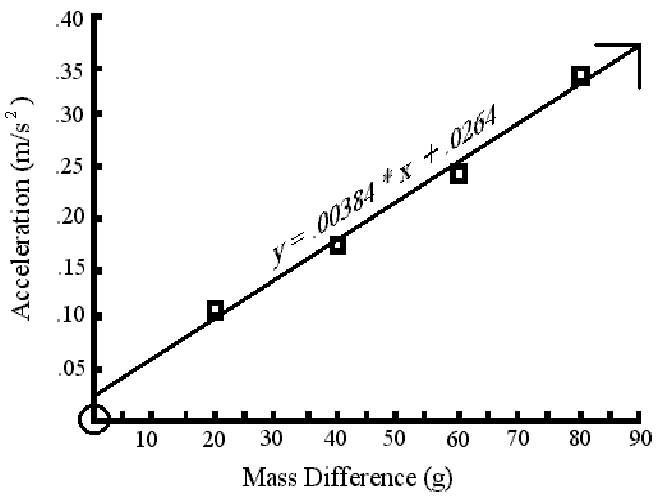
of Mass difference vs. Acceleration for part 1:
Graph
of Mass difference vs. Acceleration for part 1:
![]() Zero
acceleration
Zero
acceleration
When the mass difference is 6.88g or less the acceleration will be 0.
Using this value, the force of friction is: .364N
![]() Conclusions
Conclusions
From this lab one could conclude that Newton's third law is correct. The force on an object is dependant on both of the key factors, mass, and acceleration. I would like to comment that parts of this lab were unclear as to what measurements and calculations were required. As a result all measurements were provided for additional interpretation.
![]() Answers
to Lab Questions
Answers
to Lab Questions
1) Q: Derive an equation for the acceleration of a pulley system that accounts for a mass less, and frictionless system except for the masses of each individual side.
A: For m1 < m2: a = g * m2 / (m1 + m2).
Q: If m1 is chosen to be 93% of m2, what percent of freefall should the system have?
A: 51.8%
3) Q: Why would the tensions for T1 and T2 not be the same?
A: The tensions would be different because there would be a friction force in the pulley that would have to be accounted for. Additionally, some of the tension would have to be used as torque in order to allow the pulley to accelerate.
4) Q: What is the total effective mass undergoing an acceleration?
A: The entire system is being accelerated in some way so the mass would be that of the entire system: 2229g.
5) Q: What is the driving force producing the acceleration?
A: The driving force is the gravitational constant (g) multiplied by the heavier side's mass.
6) Q: Why were m1 and m2 chosen so that their mass was at least 1Kg?
A: The larger the mass of the entire system is, the less the acceleration will be.
7) Q: Why was the mass difference chosen to be so small?
A: The smaller the mass difference, the less the acceleration would be. If the acceleration were large, accurate measurements could not be taken.